Fibonacci
He also stumbled across a very interesting sequence of numbers while contemplating a curious problem involving rabbits. Fibonacci started with a pair of fictional and slightly unbelievable baby rabbits, a baby boy rabbit and a baby girl rabbit. They were fully grown after one month. and did what rabbits do best, so that the next month two more baby rabbits (again a boy and a girl) were born. The next month these babies were fully grown and the first pair had two more baby rabbits (again, handily a boy and a girl). Ignoring problems of in-breeding, the next month the two adult pairs each have a pair of baby rabbits and the babies from last month mature. Fibonacci asked how many rabbits a single pair can produce after a year with this highly unbelievable breeding process (rabbits never die, every month each adult pair produces a mixed pair of baby rabbits who mature the next month).

He realised that the number of adult pairs in a given month is the total number of rabbits (both adults and babies) in the previous month. He carried the calculation up to the 13th place and ended up with this sequence of numbers, which was after him named Fibonacci sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
źródło:http://oldeuropeanculture.blogspot.com/2018/02/fibonacci_24.html
Leonardo z Pizy, znany jako Fibonacci, był włoskim matematykiem z XIII wieku. W swojej 1202 książce Liber Abaci spopularyzował hindusko-arabski system liczbowy w świecie zachodnim.
Natknął się również na bardzo interesującą sekwencję liczb, rozważając ciekawy problem z udziałem królików. Fibonacci zaczynał od pary fikcyjnych i trochę niezwykłych królików, króla i królicy. Jego króliki rozmnażały się raz na miesiąc. Kolejne króliki robiły to samo, tak że w następnym miesiącu urodziły się jeszcze dwa młode króliczki (znowu chłopiec i dziewczynka). W następnym miesiącu te dzieci były w pełni dorosłe, a pierwsza para miała jeszcze dwa młode króliczki (znowu, zręcznie chłopiec i dziewczynka). Ignorując problemy związane z hodowlą, w następnym miesiącu obie pary dorosłe mają parę małych królików, a niemowlęta z ostatniego miesiąca dojrzewają. Fibonacci zapytał, ile królików może wyprodukować jedna para po roku z tym niesamowicie niewiarygodnym procesie hodowlanym (króliki nigdy nie umierają, każdego miesiąca każda dorosła para wytwarza mieszaną parę królików, które dojrzewają w następnym miesiącu).
Zdał sobie sprawę, że liczba dorosłych par w danym miesiącu jest całkowitą liczbą królików (zarówno dorosłych, jak i dzieci) w poprzednim miesiącu. Przeprowadził obliczenia do 13 sekwencji i zakończył. Sekwencja ta została po nim nazwana sekwencją Fibonacciego:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
Dividing each Fibonacci number by the previous Fibonacci number produces an interesting sequence of ratios:
Dzielenie każdej liczby Fibonacciego przez poprzednią liczbę Fibonacciego daje interesującą sekwencję stosunków:
1 / 1 = 1
2 / 1 = 2
3 / 2 = 1.5
5/3 = 1.666…
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538…
The ratio seems to be settling down to a particular value, which we call the golden ratio or the golden number usually represented by the symbol ϕ (Phi) which is an irrational (endless random decimal number) with the value 1.6180339887…
Wydaje się, że stosunek ten sprowadza się do określonej wartości, którą nazywamy złotym współczynnikiem lub złotą liczbą zwykle reprezentowaną przez symbol φ (Phi), który jest irracjonalny (nieskończona losowa liczba dziesiętna) o wartości 1.6180339887 …
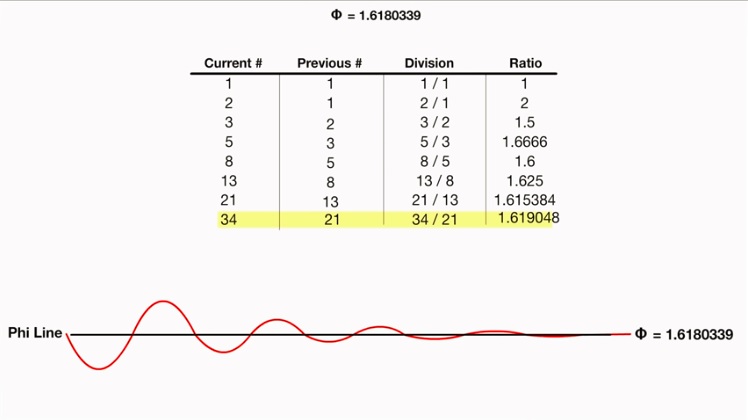
As a matter of fact, the golden ration is the most irrational number of all.
If we plot Fibonacci numbers using squares, and draw connected arches with radius equal to the size of the consecutive squares we get Fibonacci spiral.
W rzeczywistości złota proporcja jest najbardziej irracjonalną liczbą ze wszystkich. Jeśli narysujemy liczby Fibonacciego za pomocą kwadratów i narysujemy połączone łuki o promieniu równym rozmiarowi kolejnych kwadratów, otrzymamy spiralę Fibonacciego.
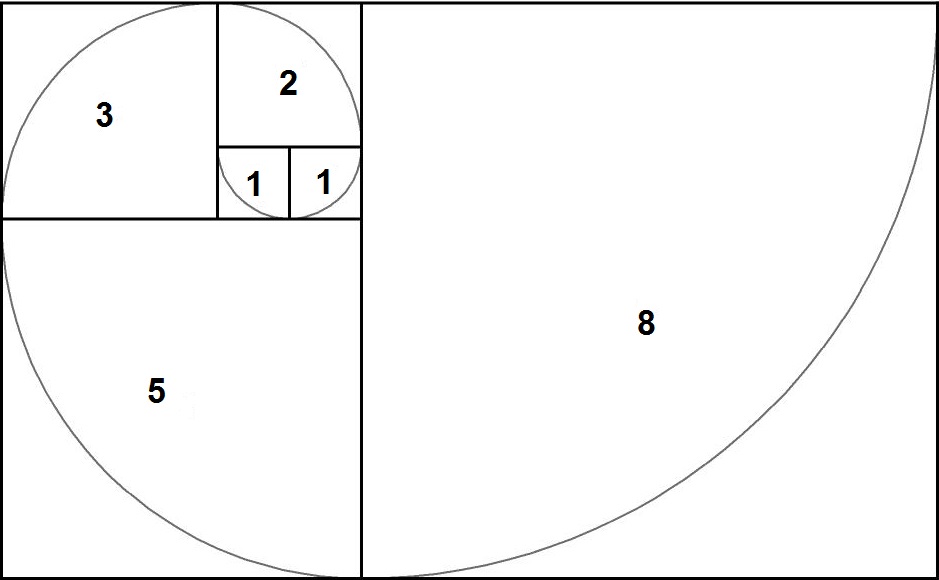
This spiral is closely related to another spiral, called the golden spiral. The golden spiral is created by plotting the equation r=e90⋅θ⋅ln(φ). This spiral grows by a factor of φ every quarter rotation. That is, if the distance from the center of the spiral to the edge of the spiral is 1 unit at some angle, then 90 degrees farther along the spiral, the distance from the center to the edge will be about 1.618 units.
