Wacław Sierpiński
| Waclaw Sierpinski | |
 1928 |
|
| Kraj działania | |
| Data i miejsce urodzenia | 14 marca 1882 Warszawa, Królestwo Polskie |
| Data i miejsce śmierci | 21 października 1969 Warszawa, Polska |
Wacław Franciszek Sierpiński (ur. 14 marca 1882 w Warszawie, zm. 21 października 1969 tamże) – polski matematyk, jeden z czołowych przedstawicieli warszawskiej szkoły matematycznej. Był jednym z twórców polskiej szkoły matematycznej.
Decyzją Międzynarodowej Unii Astronomicznej w 1976 roku imieniem Wacława Sierpińskiego został nazwany krater Sierpiński na Księżycu.
Młodość
Urodził się w rodzinie Konstantego, lekarza, i Ludwiki z Łapińskich. W 1900 ukończył V Gimnazjum Klasyczne w Warszawie i rozpoczął studia na Wydziale Fizyko-Matematycznym Cesarskiego Uniwersytetu Warszawskiego. Studia ukończył w roku 1904, uzyskując stopień kandydata nauk i złoty medal za pracę z teorii liczb na temat podany przez prof. G. F. Woronoja, a od jesieni został mianowany nauczycielem matematyki i fizyki w IV Gimnazjum Żeńskim. Uczestniczył w strajku szkolnym w 1905, porzucił pracę i wyjechał do Krakowa.
Początki kariery naukowej
W 1906 uzyskał stopień doktora filozofii na Wydziale Filozoficznym Uniwersytetu Jagiellońskiego. Po powrocie do Warszawy uczył w polskich szkołach średnich prywatnych, w Seminarium Nauczycielskim w Ursynowie oraz wykładał matematykę na Wyższych Kursach Naukowych, będących odpowiednikiem nieoficjalnego Uniwersytetu Polskiego w Warszawie.
W 1907 wyjechał na kilkumiesięczne studia do Getyngi, gdzie zetknął się z Constantinem Carathéodorym. W styczniu 1908 został członkiem Towarzystwa Naukowego Warszawskiego, a w lipcu habilitował się na Uniwersytecie Lwowskim i rozpoczął tam w 1909 wykłady z teorii mnogości jako osobnego przedmiotu.
We wrześniu 1910 otrzymał nominację na profesora nadzwyczajnego. W latach 1910-1914 wydał pierwsze swoje książki: Teoria liczb niewymiernych, Zarys teorii mnogości, Teoria liczb. Prace te zostały nagrodzone przez Akademię Umiejętności w Krakowie, która wybrała go w 1917 swoim członkiem korespondentem.
I wojna światowa
Wybuch I wojny światowej zastał go z rodziną na Białorusi w majątku teściów, Poznajowie. Jako poddany austriacki został internowany w Wiatce. Dzięki staraniom matematyków moskiewskich zezwolono mu w 1915 na przyjazd do Moskwy. Wówczas nawiązał przyjaźń i współpracę z Mikołajem Łuzinem, z którym opublikował 8 wspólnych prac. W Wiatce i Moskwie napisał I tom Analizy Matematycznej dedykując tę pracę Uniwersytetowi Polskiemu w Warszawie.
W lutym 1918 przez Finlandię i Szwecję wrócił do Polski i przez semestr letni 1918 wykładał na Uniwersytecie Lwowskim, a od jesieni 1918 wykładał już na Uniwersytecie Warszawskim, gdzie w kwietniu 1919 otrzymał nominację na profesora zwyczajnego.
Wojna polsko-bolszewicka
W czasie wojny polsko bolszewickiej, wraz z Janem Kowalewskim, brał udział w łamaniu sowieckich szyfrów[1].
Okres międzywojenny
W roku 1920 Sierpiński wspólnie z Zygmuntem Janiszewskim i Stefanem Mazurkiewiczem założyli „Fundamenta Mathematicae” – pierwsze w świecie specjalistyczne czasopismo matematyczne poświęcone teorii mnogości, jej zastosowaniom oraz logice matematycznej.
W 1921 Polska Akademia Umiejętności powołała go na członka czynnego i obdarzyła nagrodą za „Fundamenta Mathematicae”. W czasie wojny 1920 pracował w Wydziale Szyfrów Sztabu Głównego i przyczynił się do złamania sowieckiego szyfru wojskowego.
W latach międzywojennych prowadził czynne życie naukowe, wydał 8 nowych książek, dwie broszury oraz 7 podręczników szkolnych pisanych wspólnie ze Stefanem Banachem i Włodzimierzem Stożkiem.
Wacław Sierpiński był członkiem wielu towarzystw naukowych w kraju i za granicą. Od 1931 roku pełnił funkcję prezesa Towarzystwa Naukowego Warszawskiego (aż do jego wcielenia do PAN w 1952 roku). Był organizatorem i prezesem I Kongresu Matematyków Słowiańskich w Warszawie w 1929. Brał także udział jako delegat PAU w Międzynarodowych Kongresach Matematycznych w Toronto (1924), Bolonii (1928), Zurychu (1932) i Oslo (1936).
W lutym 1939 został wybrany członkiem korespondentem włoskiej królewskiej akademii nauk fizycznych i matematycznych w Neapolu[2].
II wojna światowa
Wybuch II wojny światowej zastał go w Warszawie. W okresie okupacji pracował formalnie jako urzędnik magistratu polskiego w Warszawie. Równocześnie nadal prowadził działalność dydaktyczną, wykładając w podziemnym uniwersytecie. Nie przerwał także pracy naukowej. Niektóre spośród licznych jego prac były publikowane w Sprawozdaniach Akademii Papieskiej w Rzymie; napisał też Zasady algebry wyższej (1946). W październiku 1944 mieszkanie Sierpińskich zostało spalone, wraz z nim cenna biblioteka. Po przejściu przez obóz w Pruszkowie w lutym 1945 dotarł do Krakowa.
Okres powojenny
Przez semestr letni 1945 wykładał na Uniwersytecie Jagiellońskim, jesienią wrócił na swą katedrę do Warszawy i wznowił wydawanie Fundamenta Mathematicae. W 1948 rozpoczął pracę w Państwowym Instytucie Matematycznym, a po przekształceniu tegoż w Instytut Matematyczny PAN objął w 1953 przewodnictwo Rady Naukowej Instytutu i piastował je do 1967. W 1956 objął redakcję wznowionego po przerwie wojennej pisma Acta Arithmetica i godność redaktora naczelnego piastował do 1969. Był sygnatariuszem Listu 34 (protestu przeciw cenzurze), później po represjach władzy wobec jego sygnatariuszy, był jednym z dziesięciu sygnatariuszy innego listu do The Times, zawierającego stwierdzenie, że w Polsce nie było represji, i dyskredytującego Radio Wolna Europa. Przeszedł na emeryturę z instytutu i uniwersytetu w 1960.
Wyróżnienia
Przez wszystkie te lata był bardzo aktywny naukowo. Liczba uniwersytetów, na których wykładał, wzrosła do 47; został uhonorowany wieloma odznaczeniami krajowymi i zagranicznymi; otrzymał liczne członkostwa honorowe towarzystw krajowych i członkostwa zagranicznych instytucji naukowych.
Był członkiem rzeczywistym PAN (od 1952) i jej wiceprezesem (do 1957), członkiem Międzynarodowej Akademii Filozofii Nauki w Brukseli i jej wiceprezesem (1962-1965), a także członkiem zagranicznym Accademia dei Lincei w Rzymie, Akademii Nauk w Limie i Paryżu oraz Akademii: Bułgarskiej, Czechosłowackiej, Holenderskiej, Jugosłowiańskiej, Niemieckiej, Papieskiej, Rumuńskiej i Serbskiej. Był doktorem honoris causa uniwersytetów: Uniwersytetu Jana Kazimierza we Lwowie (1929), Amsterdamie (1932), Tartu (1932), Sofijskiego w Sofii (1939)[3], Bordeaux (1947), Pradze (1948), Wrocławiu (1948), Lucknow (1949), Moskwie (1967).
Spuścizna
Pozostawił olbrzymi dorobek naukowy, obejmujący, poza wieloma książkami, 724 prace i komunikaty, 113 artykułów i 13 skryptów. Prace te dotyczyły teorii liczb, analizy matematycznej, ogólnej i opisowej teorii mnogości, topologii mnogościowej, teorii miary i kategorii oraz teorii funkcji zmiennej rzeczywistej. Szczególne znaczenie mają jego prace na temat pewnika wyboru i hipotezy continuum.
Pochowany na warszawskich Powązkach w Alei Zasłużonych.
Człowiek który dokonał w 1920 roku Cudu nad Wisłą
Dywan i Trójkąt Sierpińskiego, a Wolna Wola i Prawa RzeczyIstności, czyli Przeznaczenie
Dywan Sierpińskiego
– fraktal otrzymany z kwadratu za pomocą podzielenia go na dziewięć (3×3) mniejszych kwadratów, usunięcia środkowego kwadratu i ponownego rekurencyjnego zastosowania tej samej procedury do każdego z pozostałych ośmiu kwadratów. Nazwa pochodzi od nazwiska Wacława Sierpińskiego.
Definicja formalna
Niech  będzie kwadratem jednostkowym na płaszczyźnie kartezjańskiej
będzie kwadratem jednostkowym na płaszczyźnie kartezjańskiej 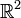 , czyli
, czyli ![D_0 = left{left(x, yright)inmathbb R^2|x, yinleft[0, 1right]right}.,](https://upload.wikimedia.org/math/a/b/f/abf724898a6e380bcbc6cd43aeb9f0ba.png) Dla danego
Dla danego  , mając zbiór
, mając zbiór 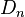 , będący sumą
, będący sumą 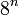 kwadratów o bokach długości
kwadratów o bokach długości  i rozłącznych wnętrzach, definiujemy zbiór
i rozłącznych wnętrzach, definiujemy zbiór  , będący sumą
, będący sumą 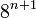 kwadratów o bokach długości
kwadratów o bokach długości  i rozłącznych wnętrzach następująco: każdy z kwadratów, których sumą jest zbiór
i rozłącznych wnętrzach następująco: każdy z kwadratów, których sumą jest zbiór 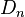 dzielimy na 9 kwadratów o bokach długości
dzielimy na 9 kwadratów o bokach długości  i rozłącznych wnętrzach i usuwamy ze zbioru
i rozłącznych wnętrzach i usuwamy ze zbioru 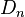 wnętrza środkowych kwadratów. Dywan Sierpińskiego D jest częścią wspólną ciągu zbiorów
wnętrza środkowych kwadratów. Dywan Sierpińskiego D jest częścią wspólną ciągu zbiorów 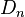 :
:
Alternatywna definicja
Dywan Sierpińskiego jest domknięciem zbioru punktów  takich że w rozwinięciu liczb
takich że w rozwinięciu liczb  i
i  w trójkowym systemie liczbowym nigdzie nie występuje cyfra 1 na tym samym miejscu po przecinku.
w trójkowym systemie liczbowym nigdzie nie występuje cyfra 1 na tym samym miejscu po przecinku.
Topologicznym dywanem Sierpińskiego nazywamy każdą przestrzeń topologiczną homeomorficzną z powyżej zdefiniowanym dywanem Sierpińskiego.
Własności dywanu Sierpińskiego
- Wymiar fraktalny dywanu Sierpińskiego wynosi ln 8/ln 3 = 1,8928…
- Pole powierzchni dywanu Sierpińskiego jest zerowe
- Dowód: W kolejnych krokach konstrukcji fraktala usuwamy z każdego z kwadratów składowych środkowy kwadrat o polu 9 razy od niego mniejszym, pozostaje zaś z niego 8 kwadratów o łącznym polu równym
 jego pola. Niech
jego pola. Niech  oznacza pole zbioru
oznacza pole zbioru  . Mamy zatem:
. Mamy zatem:
- skąd:
- Zatem dla
 dostatecznie dużych
dostatecznie dużych  jest dowolnie małe, co oznacza, że dywan Sierpińskiego zawarty jest w figurach o dowolnie małych polach powierzchni, musi zatem mieć zerowe pole powierzchni.
jest dowolnie małe, co oznacza, że dywan Sierpińskiego zawarty jest w figurach o dowolnie małych polach powierzchni, musi zatem mieć zerowe pole powierzchni.
- Dywan Sierpińskiego jest przestrzenią uniwersalną dla krzywych płaskich, tzn. każde jednowymiarowe continuum na płaszczyźnie jest homeomorficzne z podzbiorem dywanu Sierpińskiego.
Trójkąt Sierpińskiego
Trójkąt Sierpińskiego (znany też jako uszczelka Sierpińskiego) – jeden z najprostszych fraktali. Znany był na długo przed powstaniem tego pojęcia (patrz Benoît Mandelbrot). Konstrukcja tego zbioru była podana przez polskiego matematyka Wacława Sierpińskiego w 1915[1].
Trójkąt Sierpińskiego otrzymuje się następująco: w trójkącie równobocznym łączy się środki boków, dzieląc go w ten sposób na cztery mniejsze trójkąty. Trójkąt środkowy usuwa się, a wobec trzech pozostałych trójkątów operację się powtarza, dzieląc każdy z nich na cztery mniejsze trójkąty, usuwając środkowy, a wobec pozostałych czynności się powtarzają. Punkty pozostające po nieskończenie wielu powtórzeniach tej operacji tworzą trójkąt Sierpińskiego.
Fraktal ten można też utworzyć z trójkąta Pascala, zabarwiając na czarno nieparzyste jego liczby[2].
Definicja formalna
Niech  będzie trójkątem ABC.
będzie trójkątem ABC.
- Dzieląc
 na cztery mniejsze trójkąty
na cztery mniejsze trójkąty  i
i  , gdzie środki krawędzi są wierzchołkami trójkąta
, gdzie środki krawędzi są wierzchołkami trójkąta  , traktując
, traktując  jako zbiór otwarty, a trójkąty
jako zbiór otwarty, a trójkąty  za zbiory domknięte, otrzymuje się zbiory rozłączne:
za zbiory domknięte, otrzymuje się zbiory rozłączne:  i
i  . Środki krawędzi leżą w dwóch małych trójkątach (np
. Środki krawędzi leżą w dwóch małych trójkątach (np  zawiera dokładnie jeden punkt – środek odpowiedniej krawędzi).
zawiera dokładnie jeden punkt – środek odpowiedniej krawędzi). - Każdy trójkąt
 dzieli się na cztery mniejsze trójkąty
dzieli się na cztery mniejsze trójkąty  i
i 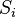 w podobny sposób.
w podobny sposób. - Każdy trójkąt
 dzieli się na cztery mniejsze trójkąty
dzieli się na cztery mniejsze trójkąty  i
i 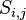 , i tak dalej.
, i tak dalej.
Trójkąt Sierpińskiego zawiera dokładnie te punkty trójkąta ABC, które nie są elementami zbioru
Wymiar fraktalny trójkąta Sierpińskiego wynosi ln 3 / ln 2 = 1,585…
Reprezentacja cyfrowa
Każdy ciąg  (gdzie
(gdzie  ) określa punkt trójkąta Sierpińskiego, a mianowicie jedyny punkt w zbiorze
) określa punkt trójkąta Sierpińskiego, a mianowicie jedyny punkt w zbiorze 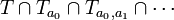 . Odwrotnie, dla każdego punktu
. Odwrotnie, dla każdego punktu  można znaleźć taki ciąg określający ten punkt, tzw. reprezentację cyfrową punktu
można znaleźć taki ciąg określający ten punkt, tzw. reprezentację cyfrową punktu  . Podobnie jak w przypadku liczb rzeczywistych, nie każdy punkt trójkąta Sierpińskiego ma jednoznaczną reprezentację. Na przykład (jedyny) punkt w przekroju
. Podobnie jak w przypadku liczb rzeczywistych, nie każdy punkt trójkąta Sierpińskiego ma jednoznaczną reprezentację. Na przykład (jedyny) punkt w przekroju  ma reprezentację
ma reprezentację  i jednocześnie reprezentację
i jednocześnie reprezentację  .
.
Trójkąt Sierpińskiego jako rezultat Gry w chaos
Ciekawym algorytmem pozwalającym otrzymać trójkąt Sierpińskiego jest gra w chaos. Narysujmy trójkąt równoboczny ABC, i definiujmy D0 := punkt A. Następnie należy wielokrotnie powtórzyć następującą operację: losowo wybieramy jeden z punktów A, B lub C, rysujemy punkt w połowie odległości między Dn i wybranym punktem. Nowo narysowany punkt oznaczamy przez Dn+1. Każdy punkt Dn będzie należeć do trójkąta Sierpińskiego, i cały trójkąt Sierpińskiego będzie prawie na pewno domknięciem zbioru {D0, D1,…}.
Jeśli wybieramy D0 nie jako punkt A, lecz jako dowolny punkt trójkąta Sierpińskiego, to znowu otrzymujemy (prawie na pewno) trójkąt Sierpińskiego. Jeśli D0 należy do trójkąta ABC ale nie do trójkąta Sierpińskiego, to żaden punkt Dn do tego trójkata nie należy, jednak otrzymujemy ten trójkąt (prawie na pewno) jako zbiór punktów skupienia ciągu (D0, D1, …).
Jeśli punkty A, B i C tworzą dowolny (nierównoboczny) trójkąt, to tą samą konstrukcją otrzymujemy zniekształcony trójkąt Sierpińskiego, tzn. obraz trójkąta Sierpińskiego przez przekształcenie afiniczne.
Gra w Chaos
Gra w chaos
Gra w chaos to algorytm komputerowego generowania obrazów pewnych fraktali. Generuje on przybliżony obraz atraktora lub punktu stałego dowolnego systemu funkcji iterowanych.
Algorytm
Zaczynając od pewnego punktu  kolejne iteracje są dane przy pomocy wzoru
kolejne iteracje są dane przy pomocy wzoru  , gdzie
, gdzie  jest jedną z funkcji iterowanych, wybieraną niezależnie i losowo dla każdej iteracji. Iteracje zbiegają się do punktu stałego systemu funkcji iterowanych. Jeżeli wartość początkowa
jest jedną z funkcji iterowanych, wybieraną niezależnie i losowo dla każdej iteracji. Iteracje zbiegają się do punktu stałego systemu funkcji iterowanych. Jeżeli wartość początkowa  należy do atraktora systemu funkcji iterowanych, wówczas wszystkie punkty
należy do atraktora systemu funkcji iterowanych, wówczas wszystkie punkty  również należą do tego atraktora i z prawdopodobieństwem 1 tworzą w nim zbiór gęsty.
również należą do tego atraktora i z prawdopodobieństwem 1 tworzą w nim zbiór gęsty.
Przykład dla trójkąta Sierpińskiego
Na początku stawia się na płaszczyźnie 3 dowolne punkty (powinny być niewspółliniowe, gdyż inaczej fraktal zdegeneruje się do odcinka), po czym wybiera sobie kolejny punkt płaszczyzny, zwany punktem gry (game point). Następnie wybiera się dowolny z trzech punktów obranych na samym początku (można je oznaczyć 1, 2 i 3, po czym korzystając z generatora liczb losowych wybierać je) i stawia punkt w połowie odległości między czwartym punktem a tym wybranym. Powtarza się ten krok, za każdym razem oznaczając punkt leżący dokładnie w połowie odległości między ostatnio postawionym a jednym z trzech pierwszych.
Efektem algorytmu – zakładając, że punkty były losowane z mniej więcej takim samym prawdopodobieństwem – jest pewien wariant trójkąta Sierpińskiego. Jego wierzchołkami są trzy punkty wybrane na samym początku gry.
Implementacja
Poniższy przykład (w języku Python) generuje trójkąt Sierpińskiego przy użyciu gry w chaos, korzystając z biblioteki pygame.
from random import * sqr = lambda a:a*a import pygame scr = pygame.display.set_mode([501, 501]) cnt = 3 pts = ( 0 + 500j, 500 + 500j, 250 + 0j, ) colors = ( (255, 0, 0), (0, 255, 0), (0, 0, 255) ) ind = randrange(cnt) pt = pts[ind] color = colors[ind] div = 2 for i in range(100000): pygame.draw.rect(scr, color, [pt.real, pt.imag, 2, 2]) newind = randrange(cnt) pt = (pt + pts[newind]) / div color = colors[newind] pygame.display.flip() while True: key = pygame.event.poll() if key.type == pygame.KEYDOWN and key.key == pygame.K_ESCAPE: pygame.quit() break pygame.time.delay(100)
Czy żyjemy w Matrixie – Macierzy RzeczyIstności? – NTV:
Czy żyjemy w hologramie? cz. 2 – Grzegorz Sławicki
Na temat Konstrukcji Wszego Świata, Rdzenia Istoty, Świadomości Nieskończonej, Wolnej Woli, Przeznaczenia i Trójkąta oraz Dywanu Sierpińskiego – zwłaszcza od 21 minuty
Dywan Sierpińskiego
Szyfrant, który sprawił Cud nad Wisłą
Są bohaterowie, których historia zapomina na długie dziesiątki lat, aby potem nieoczekiwanie oddać im sprawiedliwość. Tak historia potraktowała łodzianina Jana Kowalewskiego, szyfranta, który wraz ze swoją ekipą w znacznej mierze przyczynił się do rozgromienia wojsk sowieckich pod Warszawą w 1920 roku. Odczytywał bolszewickie depesze szybciej niż ich adresaci. Co najważniejsze, Jan Kowalewski miał talent do łamania szyfrów. Jak sam potem wspominał w Radiu Wolna Europa, szyfrantem został przez przypadek. Kolega, porucznik Stanisław Sroka, miał akurat wesele siostry. Poprosił Kowalewskiego, by zastąpił go na dyżurze w sztabie generalnym. Miał segregować depesze, które napływały z nasłuchu radiowego i wysyłać w odpowiednie miejsce. Wtedy w ręce wpadła mu sterta nierozszyfrowanych depesz bolszewickich. Dla zabicia czasu spróbował je rozszyfrować. – Wcześniej jedynym źródłem moich wiadomości o szyfrach były jedynie nowelki Allana Edgara Poe – wspominał w Wolnej Europie Jan Kowalewski. reklama – Spędziłem całą noc na tej pracy. Udało mi się rozszyfrować depesze wysłane przez tzw. „Grupę Mozyrską”. W deszyfracji pomogły mi dwie rzeczy – słowo „dywizja”, które w języku rosyjskim zawierało w sobie trzy litery „i” oraz to, że depesze były podpisywane raz szyfrem, a raz otwartym tekstem. Na drugi dzień po sztabie rozeszła wieść, że jest osoba, które potrafi rozszyfrowywać bolszewickie depesze. Janowi Kowalewskiemu kazano utworzyć komórkę deszyfracyjną przy sztabie generalnym. Założył całą sieć stacji nasłuchowych, które przy pomocy telegrafu były połączone ze sztabem głównym. Jednocześnie przy rozszyfrowaniu depesz zatrudnił znakomitych matematyków z Uniwersytetu Warszawskiego i Uniwersytetu Lwowskiego: Wacława Sierpińskiego, Stanisława Leśniewskiego, Stefana Mazurkiewicza. Już w sierpniu 1919 roku udało się im przełamać klucze szyfrowe Armii Czerwonej. Polskie dowództwo otrzymało m.in. informacje o koncentracji wojsk sowieckich, przebiegu linii frontu podczas wojny domowej na Ukrainie, i Kaukazie. Kowalewski złamał też szyfry armii Denikin i białej Floty Czarnomorskiej. – Pozwoliło to na śledzenie wydarzeń w Rosji – mówi Andrzej Rosiński. – Już w styczniu 1920 roku Kowalewski rozpoczął łamanie szyfrów niemieckich. Latem 1920 roku polscy szyfrolodzy czytali szybciej bolszewickie depesze niż ich adresaci. Jak twierdzi historyk Grzegorz Nowik, który w 2001 roku odkrył na nowo postać Kowalewskiego, to dzięki jemu i jego grupie Józef Piłsudski oraz polskie dowództwo otrzymało niesamowitą broń. W czasie bitwy warszawskiej dzięki rozszyfrowaniu depesz bolszewickich Piłsudski mógł podjąć skuteczne decyzje strategiczne. Po latach Jan Kowalewski wspominał, że Armia Konna Budionnego przełamała w 1920 roku linię frontu, co spowodowało odwrót polskich wojsk. Pierwszym sygnałem o pojawieniu się w akcji tej armii była depesza o zdobyciu polskiego pociągu pancernego. Jan Kowalewski całą noc siedział nad jej rozszyfrowaniem.
Czytaj więcej: http://www.dzienniklodzki.pl/artykul/185093,szyfrant-ktory-sprawil-cud,2,id,t,sa.html













