18 09 7524 – Lekcja 9! część 2

 

Zapis liczby 9 zmieniający się w czasie oraz Ściana Dziewięciu Smoków

9

(dziewięć) – liczba naturalna następująca po 8 i poprzedzająca 10. 9 jest też cyfrą wykorzystywaną do zapisu liczb w różnych systemach, np. w dziesiętnym i szesnastkowym systemie liczbowym.

Warunek podzielności zapisanej w systemie dziesiętnym liczby przez 9 to, aby suma cyfr w danej liczbie była podzielna przez 9, np.

123456789 → 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45

45 → 4 + 5 = 9

Dlatego więc 9 pomnożone odtwarza się stale 9 x 2 = 18, 1 + 8 = 9, 9 x 3 = 27, 2 + 7 = 9 itd.

Dziewięć jest podzielne przez dziewięć, więc liczba 123456789 jest podzielna przez 9.

 

9

9  było i jest symbolem przeczucia, odrodzenia, duchowości i podróży.

W mitologii greckiej uchodziła za liczbę rytualną – dziewięć dni trwały misteria eleuzyńskie na cześć bogini ziemi – Demeter; u Homera w orszaku Apollina występowało dziewięć muz. Hezjod utrzymywał, że aby dostać się do nieba, trzeba wędrować dziewięć dni i dziewięć nocy. Za najdoskonalszy wiek, jaki mógł osiągnąć człowiek uważano 81 lat – iloczyn dwóch dziewiątek.

W chrześcijaństwie dziewięć dni trwa nowenna. Dziewięć jest chórów anielskich, a grzesznicy wchodzą do piekła przez dziewięć bram: trzy spiżowe, trzy kamienne i trzy żelazne. W chrześcijaństwie 9 uchodzi za liczbę absolutnej doskonałości (3 pomnożone przez 3)^{[potrzebne źródło]}.

W islamie dziewięć otworów jakie ma ciało ludzkie jest uważane za symbol kontaktu człowieka ze światem zewnętrznym, muzułmański sznur modlitewny subha ma 99 paciorków, a Allah występuje w Koranie pod 99 imionami.

W kulturze Japonii dziewiątka jest liczbą przynoszącą szczęście i długie życie. Za przykład służą np. skrytobójcy, którzy zawsze nosili ze sobą 9 noży do rzucania

Jeden

Od dawnych czasów liczba 1 była uważana za najdoskonalszą. Jest ona pierwszą liczbą nieparzystą. Wszystkie następne liczby pochodzą od niej, np. 2 = 1 + 1. Nie można powiedzieć jednoznacznie, czy jeden to jest dużo czy mało? Pierwszym chce być każdy w wielu dziedzinach, ale jeżeli chodzi o dostanie jedynki ze sprawdzianu, to nie chce jej nikt.

Dwa

Kolejna liczbą jest 2. Jest ona parzysta. Dawno temu ludzie uważali ją za złowieszczą. Byli nią oznaczani szpiedzy, policjanci czy wysłannicy. Patrząc na nią z innej strony, zobaczymy, że ściśle wiąże się z człowiekiem, ponieważ ma on 2 oczu, 2 uszu, 2 ręce, 2 nogi. Wszyscy z pewnością znają powiedzenie: „Gdzie dwóch się bije, tam trzeci korzysta”.

Trzy

Następna liczbą jest 3. Jest ona nieparzysta, wierzy się, że przynosi ona szczęście. Często była wykorzystywana przez pisarzy czy wróżki. Znanymi trójkami są: 3 muszkieterowie, 3 wróżki, do trzech razy sztuka, czy raz, dwa, trzy start!, natomiast mówić „trzy po trzy” znaczy, że ktoś mówi bez sensu.

Cztery

Liczba cztery była uważana za świętą, głównie w starożytnej Grecji. Mamy 4 strony świata, 4 pory roku, szczęśliwcem jest ten, kto znajdzie czterolistną koniczynę, ponieważ przynosi ona szczęście. Mówi się również „spadać na 4 łapy” o człowieku, który bez szwanku wychodzi z każdej sytuacji.

Pięć

Również pięć była uważana za szczęśliwą. Między innymi była symbolem potęgi Boga oraz człowieka (symbol z rozstawionymi rękami nogami i głową). W ciele człowieka można wyróżnić następujące piątki: palce u jednaj ręki czy nogi, człowiek ma pięć zmysłów: słuch, wzrok, węch, smak i dotyk. Znanymi powiedzeniami są: „ni w pięć nie w dziewięć” co znaczy – bez sensu, czy „piąte koło u wozu” o rzeczy zbędnej.

Sześć

Kolejną szczęśliwą liczbą jest liczba sześć oraz jest symbolem szczęścia i pokoju. W Biblii możemy przeczytać, że Bóg stworzył świat w sześć dni. W Polsce dawniej bito monetę ze srebra o wartości sześć groszy. Najwyższą oceną w szkole jest szóstka.

Siedem

Liczba siedem jest liczbą szczęśliwą i magiczną. Tydzień ma siedem dni, siódmym dniem tygodnia jest niedziela, czyli dzień świąteczny, ludzie wierzą również, że coś miłego spotka nas siódmego dnia miesiąca, czy że w konkursie będziemy zali odpowiedz na siódme pytanie. Z siódemką wiąże się również „ocet siedmiu złodziei” co oznacza kogoś niezadowolonego lub „od siedmiu boleści” co oznacza coś bez wartości. W wielu bajkach mamy liczbę siedem, np. siedmiu krasnoludków czy 7 braci, których zaklęto w czarne kruki. Mamy również siedem cudów świata.

Osiem

Ósemka jest symbolem doskonałości i nieskończoności. Duże znaczenie ma w religii chrześcijan. Na Arce Noego było ośmiu członków załogi: Noe z żoną, jego trzej synowie i ich żony. Liczbę osiem symbolizują splecione dwa węże kaduceusza, czyli laski herolda uważanej za czarodziejską. Wiją się na niej 2 węże, które patrzą siebie w oczy. W matematyce symbol nieskończoności to leżąca ósemka. Gdy ludzie mówią, że coś jest ósmym cudem świata, znaczy, że jest to coś wspaniałego i budzi to powszechny podziw.

Dziewięć

Szczęśliwą liczbą jest również 9, ponieważ pomnożona odtwarza się stale. Zobaczmy:

2 * 9 = 18 gdy zsumujemy jej cyfry dostaniemy: 1 + 8 = 9

3 * 9 = 27 gdy zsumujemy jej cyfry dostaniemy: 2 + 7 = 9

4 * 9 = 36 gdy zsumujemy jej cyfry dostaniemy: 3 + 6 = 9

5 * 9 = 45 gdy zsumujemy jej cyfry dostaniemy: 4 + 5 = 9

6 * 9 = 54 gdy zsumujemy jej cyfry dostaniemy: 5 + 4 = 9

7 * 9 = 63 gdy zsumujemy jej cyfry dostaniemy: 6 + 3 = 9

8 * 9 = 72 gdy zsumujemy jej cyfry dostaniemy: 7 + 2 = 9

9 * 9 = 81 gdy zsumujemy jej cyfry dostaniemy: 8 + 1 = 9

Liczba dziewięć była również chętnie wykorzystywana w bajkach i magii.

• Literom A, Ą, J, S, Ś jest przypisana cyfra 1.
• Literom B, K, T jest przypisana cyfra 2.
• Literom C, Ć, L, Ł, U jest przypisana cyfra 3.
• Literom D, M, V, jest przypisana cyfra 4.
• Literom E, Ę, N, Ń, W jest przypisana cyfra 5.
• Literom F, O, Ó, X jest przypisana cyfra 6.
• Literom G, P, Y jest przypisana cyfra 7.
• Literom H, Q, Z, Ż, Ź jest przypisana cyfra 8.
• Literom I , R jest przypisana cyfra 9.

Według numerologii „liczba urodzenia” determinuje cechy osoby, i tak:

• 1 – to człowiek o cechach przywódczych, pionier przecierający innym szlaki, indywidualista, człowiek o silnej „wibracji”, mocno zaznaczający swoją obecność, eksponujący swoje ego,
• 2 – to „dyplomata” mający świadomość dwóch obliczy świata, zainteresowany drugim człowiekiem, wrażliwy, kierujący się w życiu uczuciami,
• 3 – to człowiek ukierunkowany na osobiste spełnienie, o dużych talentach i możliwościach w każdej dziedzinie, we wszystkim co robi widać wolę działania, siłę, przedsiębiorczość oraz kreatywność. Ponieważ jednak jest zwykle osobą świecącą „światłem odbitym”, to kiedy jest słabo ukierunkowana, zdeterminowana, trudno jej się odnaleźć,
• 4 – to logik osiągający najwięcej dzięki wytrwałości w zdobywaniu wiedzy, bardzo odporny na stres związany z pracą,
• 5 – to osoba chętnie ucząca się nowych rzeczy, otwarta na nowinki, mająca dużą łatwość w zdobywaniu wiedzy, wielką zmysłowość oraz związaną z tym skłonność do używek,
• 6 – to osoba rodzinna, uważająca rodzinę za fundament swojego życia i mocno z nią związana. Jest zwykle kreatywna intelektualnie, ma łatwość odnajdywania się w przestrzeni i czasie, nie lubi stawiać sobie ograniczeń, jest bardzo uczuciowa i wrażliwa,
• 7 – to osoba wrażliwa i introwertyczna, łatwo robiąca karierę zawodową, bardzo zainteresowana sprawami duchowymi. Zbyt silna siódemka powoduje nadmierne przywiązanie do materii,
• 8 – to twórca na dużą skalę, energia zmieniająca się w materię, osoba tworząca i działająca poprzez podświadomość, uparta i zdeterminowana w działaniu,
• 9 – to osoba opierająca swoje działanie na bezinteresownej miłości, posiadająca „wibrację” spełnienia.

Biblijna

1	wyjątkowość, zwłaszcza w odniesieniu do Boga	Pwt 6,4; 2 Krl 19,15
2	potwierdzenie, pewność	Rdz 41,32; Iz 40,2; Hbr 6,18
3	nasilenie, podkreślenie znaczenia	Iz 6,3; Jr 7,4
4	porządek w odniesieniu do spraw ziemskich, powszechność	Rdz 2,10
6	niedoskonałość, niepełność	2 Sm 21,20; Ap 13,18
7	pełnia, całość, doprowadzenie czegoś do końca	Jz 6,2–4,15; Ap 5,1–6
8	doskonałość, nieskończoność, obfitość	Mi 5,5 (5,4, BT)

Poniżej znajduje się opis znaczenia liczb w numerologii chińskiej. Każda liczba ma swoje miejsce w kwadracie numerologicznym znajdując się na przecięciu jednej z trzech pionowych stref kwadratu numerologicznego i jednego z trzech poziomych planów.

Jedynka

3	6	9
2	5	8
1	4	7

W wielu kulturach uważana za liczbę doskonałą, reprezentującą niewidzialną, ale aktywną siłę twórczą leżącą u podstaw wszystkiego co istnieje. Symbolizuje ona również nasze ego i świadomą aktywność, a także początek przedsięwzięć i ważnych etapów życia. Związana jest ona z naszą indywidualnością i jej przeżywaniem. Może oznaczać zarówno samodzielność jak i samotność w zależności od tego czy przejawia się ona w sposób harmonijny czy nieharmonijny.

Dwójka

3	6	9
2	5	8
1	4	7

Dwójka oznacza harmonijne współdziałanie przeciwieństw symbolizowane przez yin i yang. Starożytni mędrcy doskonale zdawali sobie sprawę, że właściwe funkcjonowanie świata i człowieka zapewniane jest przez współdziałanie przeciwstawnych sił i tendencji. Znaczenie liczby dwa stanowi więc harmonia, porządek, umiejętność zatroszczenia się nie tylko o siebie ale i o innych ludzi, umiejętność godzenia skłóconych poprzez podejmowanie się mediacji, a również równowaga i umiarkowanie.

Trójka

3	6	9
2	5	8
1	4	7

Liczba 3 jest symbolem intuicji, magii, sił twórczych i radości, którą niesie korzystanie z nich. Reprezentuje ona również Czas, składający się z trzech elementów: już poznanego i doświadczonego zwanego Przeszłością, właśnie przeżywanego zwanego Teraźniejszością oraz nieznanego i niepewnego, zwanego Przyszłością. W ten sposób symbolizuje ona przeistaczanie się tego co znane aby wyłonić rzeczy nowe i nieznane, czyli siły twórcze drzemiące w każdym z nas.

Czwórka

3	6	9
2	5	8
1	4	7

Czwórka to liczba stabilności i porządku. Wszystkie procesy, nawet te bardzo dynamiczne zachodzą w pewnych ramach czasowych i przestrzennych (cztery strony świata, cztery pory roku). Ramy te pozostają niezmienne. Cyfra 4 oznacza również dom, spokój i solidność. Reprezentuje także powtarzalność i nieuchronność.

Piątka

3	6	9
2	5	8
1	4	7

Piątka to liczba podróżników, poszukiwaczy i odkrywców. Symbolizuje ona ruch, zmianę i nieprzewidywalność. Znaczenie liczby 5 wskazuje na ogrom chaosu w przyrodzie a także na jego dzikie piękno i potęgę. Zmiana, dzikość i nieprzewidywalność wiążą się także z omylnością i poszukiwaniem.

Szóstka

3	6	9
2	5	8
1	4	7

Znaczeniem liczby sześć jest równowaga, harmonia, miłość i prawda. Symbolizuje ona natchnienie i pomysły pojawiające się w naszym umyśle w chwilach relaksu, odprężenia i wewnętrznej harmonii. Liczba ta przypomina również swoim znaczeniem o konieczności wybaczania, które łatwiej przychodzą nam właśnie w lżejszych stanach świadomości.

Siódemka

3	6	9
2	5	8
1	4	7

Siódemka jest najbardziej tajemniczą z wszystkich cyfr. Podobnie jak cyfra trzy, siódemka jest liczbą magiczną. O ile jednak trójka symbolizuje siły magiczne w akcji o tyle siódemka reprezentuje ezoteryczny aspekt magii – dający zrozumienie nielicznym, którzy są do niego zdolni. Znaczenie siódemki związane jest z wyobraźnią, świadomą myślą i koncentracją.

Ósemka

3	6	9
2	5	8
1	4	7

Znaczenie liczby osiem związane jest z przedsięwzięciami i ich sukcesem. Symbolizuje determinację i wytrwałe dążenie do celu, a także uporządkowanie spraw niezbędne do jego osiągnięcia. W Chinach jest uważana za liczbę bardzo szczęśliwą. Łączy w sobie dwie cechy: jest liczbą parzystą, co symbolizuje pełnię i jednocześnie jest największą cyfrą parzystą, stąd jej znaczenia dotyczące sukcesu i realizacji celów.

Dziewiątka

3	6	9
2	5	8
1	4	7

Dziewiątka reprezentuje stan osiągnięcia pełni w jakiejś dziedzinie. Związana jest z wysokim poziomem rozwoju intelektualnego, emocjonalnego bądź duchowego. Daje kontrolę nad własnym losem i wpływ na losy innych ludzi. Symbolika tej cyfry przypomina, że każdy z nas ma w sobie potencjał aby zmienić coś w otaczającym nas świecie na lepsze. Jej znaczenie związane jest z wynalazczością, pomysłowością i skutecznością. Jest to liczba zamykająca cykl numerologiczny a tym samym stawiająca podstawy do rozpoczęcia kolejnego.

 

Dywan i Trójkąt Sierpińskiego, a Wolna Wola i Prawa RzeczyIstności, czyli Przeznaczenie

Dywan Sierpińskiego

 

– fraktal otrzymany z kwadratu za pomocą podzielenia go na dziewięć (3×3) mniejszych kwadratów, usunięcia środkowego kwadratu i ponownego rekurencyjnego zastosowania tej samej procedury do każdego z pozostałych ośmiu kwadratów. Nazwa pochodzi od nazwiska Wacława Sierpińskiego.

Definicja formalna

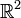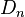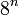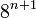Niech będzie kwadratem jednostkowym na płaszczyźnie kartezjańskiej , czyli Dla danego , mając zbiór , będący sumą kwadratów o bokach długości i rozłącznych wnętrzach, definiujemy zbiór , będący sumą kwadratów o bokach długości i rozłącznych wnętrzach następująco: każdy z kwadratów, których sumą jest zbiór 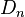dzielimy na 9 kwadratów o bokach długości i rozłącznych wnętrzach i usuwamy ze zbioru 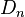wnętrza środkowych kwadratów. Dywan Sierpińskiego D jest częścią wspólną ciągu zbiorów :

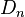Alternatywna definicja

Dywan Sierpińskiego jest domknięciem zbioru punktów takich że w rozwinięciu liczb i w trójkowym systemie liczbowym nigdzie nie występuje cyfra 1 na tym samym miejscu po przecinku.

Topologicznym dywanem Sierpińskiego nazywamy każdą przestrzeń topologiczną homeomorficzną z powyżej zdefiniowanym dywanem Sierpińskiego.

Własności dywanu Sierpińskiego

• Wymiar fraktalny dywanu Sierpińskiego wynosi ln 8/ln 3 = 1,8928…
• Pole powierzchni dywanu Sierpińskiego jest zerowe

Dowód: W kolejnych krokach konstrukcji fraktala usuwamy z każdego z kwadratów składowych środkowy kwadrat o polu 9 razy od niego mniejszym, pozostaje zaś z niego 8 kwadratów o łącznym polu równym jego pola. Niech oznacza pole zbioru . Mamy zatem:

skąd:

Zatem dla dostatecznie dużych jest dowolnie małe, co oznacza, że dywan Sierpińskiego zawarty jest w figurach o dowolnie małych polach powierzchni, musi zatem mieć zerowe pole powierzchni.

• Dywan Sierpińskiego jest przestrzenią uniwersalną dla krzywych płaskich, tzn. każde jednowymiarowe continuum na płaszczyźnie jest homeomorficzne z podzbiorem dywanu Sierpińskiego.

Trójkąt Sierpińskiego

Definicja formalna

Niech będzie trójkątem ABC.

• Dzieląc na cztery mniejsze trójkąty i , gdzie środki krawędzi są wierzchołkami trójkąta , traktując jako zbiór otwarty, a trójkąty za zbiory domknięte, otrzymuje się zbiory rozłączne: i . Środki krawędzi leżą w dwóch małych trójkątach (np zawiera dokładnie jeden punkt – środek odpowiedniej krawędzi).
• Każdy trójkąt dzieli się na cztery mniejsze trójkąty i 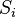w podobny sposób.
• Każdy trójkąt dzieli się na cztery mniejsze trójkąty i 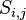, i tak dalej.

Trójkąt Sierpińskiego zawiera dokładnie te punkty trójkąta ABC, które nie są elementami zbioru

Wymiar fraktalny trójkąta Sierpińskiego wynosi ln 3 / ln 2 = 1,585…

Reprezentacja cyfrowa

Każdy ciąg (gdzie ) określa punkt trójkąta Sierpińskiego, a mianowicie jedyny punkt w zbiorze 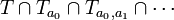. Odwrotnie, dla każdego punktu można znaleźć taki ciąg określający ten punkt, tzw. reprezentację cyfrową punktu . Podobnie jak w przypadku liczb rzeczywistych, nie każdy punkt trójkąta Sierpińskiego ma jednoznaczną reprezentację. Na przykład (jedyny) punkt w przekroju ma reprezentację i jednocześnie reprezentację .

Trójkąt Sierpińskiego jako rezultat Gry w chaos

Ciekawym algorytmem pozwalającym otrzymać trójkąt Sierpińskiego jest gra w chaos. Narysujmy trójkąt równoboczny ABC, i definiujmy D₀ := punkt A. Następnie należy wielokrotnie powtórzyć następującą operację: losowo wybieramy jeden z punktów A, B lub C, rysujemy punkt w połowie odległości między D_n i wybranym punktem. Nowo narysowany punkt oznaczamy przez D_n+1. Każdy punkt D_n będzie należeć do trójkąta Sierpińskiego, i cały trójkąt Sierpińskiego będzie prawie na pewno domknięciem zbioru {D₀, D₁,…}.

Jeśli wybieramy D₀ nie jako punkt A, lecz jako dowolny punkt trójkąta Sierpińskiego, to znowu otrzymujemy (prawie na pewno) trójkąt Sierpińskiego. Jeśli D₀ należy do trójkąta ABC ale nie do trójkąta Sierpińskiego, to żaden punkt D_n do tego trójkata nie należy, jednak otrzymujemy ten trójkąt (prawie na pewno) jako zbiór punktów skupienia ciągu (D₀, D₁, …).

Jeśli punkty A, B i C tworzą dowolny (nierównoboczny) trójkąt, to tą samą konstrukcją otrzymujemy zniekształcony trójkąt Sierpińskiego, tzn. obraz trójkąta Sierpińskiego przez przekształcenie afiniczne.

Gra w Chaos

 

Gra w chaos

Gra w chaos to algorytm komputerowego generowania obrazów pewnych fraktali. Generuje on przybliżony obraz atraktora lub punktu stałego dowolnego systemu funkcji iterowanych.

 

Algorytm

Zaczynając od pewnego punktu kolejne iteracje są dane przy pomocy wzoru , gdzie jest jedną z funkcji iterowanych, wybieraną niezależnie i losowo dla każdej iteracji. Iteracje zbiegają się do punktu stałego systemu funkcji iterowanych. Jeżeli wartość początkowa należy do atraktora systemu funkcji iterowanych, wówczas wszystkie punkty również należą do tego atraktora i z prawdopodobieństwem 1 tworzą w nim zbiór gęsty.

Przykład dla trójkąta Sierpińskiego

Na początku stawia się na płaszczyźnie 3 dowolne punkty (powinny być niewspółliniowe, gdyż inaczej fraktal zdegeneruje się do odcinka), po czym wybiera sobie kolejny punkt płaszczyzny, zwany punktem gry (game point). Następnie wybiera się dowolny z trzech punktów obranych na samym początku (można je oznaczyć 1, 2 i 3, po czym korzystając z generatora liczb losowych wybierać je) i stawia punkt w połowie odległości między czwartym punktem a tym wybranym. Powtarza się ten krok, za każdym razem oznaczając punkt leżący dokładnie w połowie odległości między ostatnio postawionym a jednym z trzech pierwszych.

Efektem algorytmu – zakładając, że punkty były losowane z mniej więcej takim samym prawdopodobieństwem – jest pewien wariant trójkąta Sierpińskiego. Jego wierzchołkami są trzy punkty wybrane na samym początku gry.

Implementacja

Poniższy przykład (w języku Python) generuje trójkąt Sierpińskiego przy użyciu gry w chaos, korzystając z biblioteki pygame.

Żart ale nie do końca – Pamiętacie Iskon Ukraiński? Kolejna kometa Iskonu? 27 09 7524 = 9-9-9