Rafał Kopko Orlicki – Jaki system liczbowy posiadali Prasłowianie?

Współcześnie, posługujemy się systemem dziesiętnym. Jednak w przypadku dawnych Słowian, krążą przekazy o nieco dłuższym układzie liczbowym, bo dwunastkowym.
Może to wynikać z odzwierciedlenia w nim, podziału roku na dwanaście miesięcy. Rok taki miał jeszcze (to bardzo prawdopodobne) u Słowian miesiąc trzynasty, wyraźnie krótszy, W ten sposób, Słowianie mieli niwelować różnice pomiędzy rokiem księżycowym a słonecznym.
https://wiaraprzyrodzona.wordpress.com/kalendarz-slowian/
https://opolczykpl.wordpress.com/kalendarz-slowian/
https://wiaraprzyrodzona.wordpress.com/2018/01/03/przynaleznosc-miesiecy-i-skad-sie-one-biora/
https://pl.wikipedia.org/wiki/Kalendarz_s%C5%82owia%C5%84ski
https://www.slawoslaw.pl/cykl-roczny/kalendarz/
Pamiętam, jak niedawno jeszcze wyczytywałem na Wikipedii, jakoby rzekomo Słowianie potrafili liczyć tylko do pięciu, bo drugą ręką zawsze trzymali wodze swojego rumaka. Z jednej strony świadczyło to o udomowieniu przez Słowian konia z którego podobno nigdy nie schodzili. Nawet gdy chcieli coś policzyć. I o kompletnej nieznajomości autora tego twierdzenia, jazdy konnej. Bo każdy kto ją uprawiał, wie, że można liczyć na palcach obu rąk bez problemu z wodzami.
A moim zdaniem, Słowianie licząc do dwunastu, korzystali z całego zakresu rąk, bo nie tylko palców, lecz dodatkowo jednego i drugiego przedramienia.
Gdzie ręce skrzyżowane, pokazujące pełen dolny i górny trójkąt, oznaczały liczbę12-cie.
Zaś ręce połączone w dłoniach tworzyły znak trójkąta wzniesionego wierzchołkiem do góry, podobnego do cyfry 1, oznaczając liczbę 11, zarazem dzień.
Liczbę 10 oznaczały moim zdaniem ramiona połączone poprzez uchwycenie dłonią łokcia drugiej ręki. Obojętnie której, tworzyły znak L, trójkąt nieco odwrócony, lekko otwarty do góry. Lub po prostu obie zaciśnięte dłonie obok siebie.
W taki sposób powstał system dwunastkowy, dawno dostrzegany przez Słowian w naturze.
Dwanaście miesięcy roku, to zauważmy, podział przyjęty przez zachód, nie wprowadzony jednak przezeń do systemu liczbowego. Tam mamy dziesiętny.
W przypadku posiadania systemu 12-kowego, konsekwentnie, każda liczba u Słowian mogła dzielić się na dwanaście części, ułamków. W efekcie, dzień, na 12-cie „godzin”, podobnie noc. Mieliśmy wówczas 24 godziny na dobę. I to jest zapewne prawdziwe pochodzenie dzisiejszego, „zachodniego” podziału godzinowego doby. Bo nie ma on nic wspólnego z zachodnim systemem dziesiętnym.
System, rozdzielający liczbę 1-en na jeszcze mniejsze elementy, znajdujemy w od aryjskich Wedach, gdzie wymienia się bardzo krótkie jednostki czasu, pozwalające mierzyć zjawiska kosmiczne, wręcz prędkość światła. Warto zwrócić uwagę, że prędkość światła która wynosi 299 792 km/s , dzielona przez 12-cie, to niemal 24 … Niemal, bo brakuje tego trzynastego elementu, po przecinku, dla ścisłej rachuby.
Mamy również cykl liczbowy jakim jest okres roczny. Rok słoneczny lub gwiezdny, liczy w przybliżeniu 365 dni, plus parę godzin. Natomiast rok księżycowy, 354 plus parę godzin.
Dzieląc roki; słoneczny, gwiezdny i księżycowy przez 10, uzyskamy bardzo niedokładny wynik. Dzieląc je przez 12-cie , wynik ten będzie już bardziej dokładny w sensie uzyskania jednej liczby bez cyfr po przecinku. Najbliższy wówczas tej pełni wynik, przyniesie podział dokonany na roku księżycowym. Gdy jednak zwiększymy liczbę użytą do dzielenia, o trzynasty element, np. 0,2 (12,2), w przypadku roku księżycowego uzyskamy wynik niemal idealny.
Zauważmy też, że znak 10 oznaczający w obecnym systemie dziesiętnym ostatnią liczbę, stanowią dwie cyfry; 1 + 0. Zero, to dawniej nie liczba, tylko cyfra. Nie liczy się z użyciem cyfry zero,bo zawsze daje to zero (mnożenie) lub drugą cyfrę operowaną; 1-0=1, 1+0=1.
Cyfra ta, u Słowian oznaczała początek, koniec lub środek, dla czegokolwiek. Stąd jej sanskrycka lecz późna nazwa 'sunja’ lub 'śuunja’ (pusta). Nie pochodzi jednak z Wed i jedynie nieznacznie oddaje to pierwotne znaczenie, swoją pokrewną nazwą. Przeniesiona do perskiego jako sirja (pustka), arabskiego jako sifr/sifrja, i odmieniona w Europie w sifro/siro a następnie ziro/zero. Tylko Niemcy nie poszanowali tej nazwy, nazywając ją null (nic), ale oddając jej sens. Ta cyfra nic nie zawiera. Jest pustką. Dlatego w sanskrycie oznaczano ją jako koło z kropką lub malutkie kółeczko. Jej sens jak i nazwa, ma ścisłe pochodzenie z języka arjowego, prasłowiańskiego. Tak zrozumiała w naszym języku polskim ; ś-rodek ; światło – rodzi. Siła stwórcza, początek. To był znak rozdzielający, zaczynający, lub kończący. Nie pustka!
Jakby Słowianie nie wierzyli w jakąkolwiek pustkę, absolutną próżnię. Co nauka potwierdza, bo okazuje się, że w próżni też są cząstki energii. Jak to przewidział Tesla.
Kontynuatorzy sanskrytu w Indiach, nadali jej nazwę odbiegającą od tego pierwotnego znaczenia, acz pochodną z języka arjowego, gdzie sens był podobny. Jakby; sun – nija ; światło/słońce – nicości. Czyli również początek a nie pustka.
Cyfra ta, wraz z innymi, zatoczyła koło, rodem z Vincza (gdzie też mamy znaki koła) do Rasenii/Etrurii będącej na zachodniej stronie cypla włoskiego pod wpływami Vincza (widziana w niektórych oznaczeniach jako kropka dzieląca zdania i wyrazy, podobnie jak dwie pionowe kreski), do Kujaw a stamtąd do Indii, z nich do Persji, stamtąd do Arabii w czasie podbojów islamskich, stamtąd z kolei do Hiszpanii podbitej przez Arabów, stąd do Włoch. Gdzie celowo zniszczono lub zapomniano pismo i liczebniki etruskie, jako pochodne ze wschodu od Słowian – Arjów. W epoce narzucania propagandą religijną Rzymu chrześcijańskiego, wszystkiego z zachodu, jako rzekome osiągnięcie cywilizacji łacińskiej, litery pochodzące z Etrurii bliskie Słowianom bo pochodne z kultury Vincza, nazwano łacińskimi a cyfry pochodzące również z tej strony, nazwano arabskimi. Wszystko na opak. Byle nie słowiańskimi, nie od nazwy podbijanych ludów pogańskich, nie wierzących w święte księgi, częściowo wspólne dla; Żydów, Chrześcijan, Arabów.
Cytat: „Już w VII w. p.n.e. Babilończycy stosowali zero jako cyfrę w zapisie pozycyjnym, ale nigdy nie występowało ono samodzielnie jako liczba. W cywilizacji Majów zero było znane jako liczba już w I w. p.n.e. (być może znali je już w IV wieku p.n.e. wchłonięci przez Majów Olmekowie).
W roku 130 zera używał Klaudiusz Ptolemeusz. Współczesne pojęcie zera przypisuje się Hindusowi Brahmagupcie, a pierwsze wzmianki pochodzą z roku 628. Zero stosowano niekonsekwentnie również w średniowieczu, nie miało ono jednak swojej reprezentacji w cyfrach rzymskich – stosowano łacińskie słowo nullae. „
Znak 10, jest więc takim jakim jest, bo nie potrafiono lub nie chciano przywrócić jego pierwotnego wyglądu, w jakim nie było zera – 0. Tylko jedna cyfra.
Dzisiaj, mamy w 10-ce cyfry dwie, jakby zaczynała ona kolejny porządek. A zaczyna go przecież liczba dwucyfrowa 11.
10 sugeruje również wzrokowo, że chodzi o 1 + 0. A takie połączenie daje 1. Brakuje więc tutaj prawdziwej, dawnej cyfry.
U Etrusków był to znak X.
Lecz nie u Vinczan.
U nich, cyfrę 10 stanowiły moim zdaniem, dwa odwrócone, zamknięte i połączone trójkąty.
Podobne przekręcenia mamy w innych cyfrach.
Dzisiaj, używamy w piśmie zwanym rzymskim, dla cyfry 5, znaku V. U Etrusków był ten trójkąt odwrócony. To Rzymianie ją przekręcili. Tak nienawidzili wszystkiego co etruskie. Za lata niewoli.
Chrześcijanie z kolei odrzucili niemal wszystkie znaki raseńskie/etruskie, od – vińczańskie, prasłowiańskie, arjowe, poza niektórymi i poprzekręcanymi, używając ich jedynie w oznaczeniach na swoich budowlach, w tradycji rzymskiej.
Stąd, z etruskiego przetrwały tylko pięć cyfr; 1, 5, 10, 50, 100. Jest nieprawdopodobne, aby ci zręczni budowniczowie akweduktów, łaźni i pierwszych domów kopułowych z kamienia, nie potrafili precyzyjnie liczyć. Do czego potrzebny był im pełen układ liczbowy.
A ich nazwa dla 10 zapisywanej jako X, odczytana w wymowie jako „śar”, jest prawidłowa, blisko spokrewniona z pierwotną. To najpewniej nazwa dla cyfry 4 . Pochodząca od 'tśar/ćśar/czar/czarń/czarny’ dla oznaczenia pory nocy, (stąd; tśari/tśeri/cztery/cztjeri > czerty/kreśl/kreski). Raseni często opuszczali pierwsze głoski z wyrazów słowiańskich , z jakich pochodziły terminy etruskie.
„Śar” pochodzi od cyfry po – trzeciej; tsi/tśi/trsi/tsi/tri/trzy.
Cyfra jaką dzisiaj znamy jako rzymską dziesiątkę, oznaczaną znakiem X, pierwotnie , nie oznaczała pełni układu liczbowego. To, zapewne skrócona forma dla cyfry cztery 4.
Pełnią układu liczbowego było 12-cie lub 12-cie + ułamek! Ta wspomniana na początku L
Dzisiaj, znak L, przypisywany jest rzymianom jako 50.
Takie nastąpiło zamieszanie w znakach cyfrowych. Pierwotne formy arabskie, przejęte z sanskrytu zmienionego w Persji (rozpropagował te cyfry w Afryce perski a nie arabski matematyk Al Chawurazim, zaś w Europie – Włoch, Leonardo Bonacci, ), często zupełnie nie przypominają naszych obecnych cyfr tzw. arabskich. Mówienie więc, że są to cyfry arabskie, jest podwójnie nieprawdziwe. Raz, bo pierwotnie nie pochodzą z Arabii. Dwa, bo nie wszystkie odzwierciedlają cyfry, jakimi się posługujemy – mające swoje odbicie w piśmie vinczańskim bardziej niż arabskim.
Matematyka zgłosiła problem liczb pierwszych. Przebadałem je nieco pod kątem dojścia jakiegoś sensu dla liczby 12-cie lub 13-cie lub ułamka z nimi, dla zrozumienia powtarzanego w naturze porządku, bez konieczności sztucznego dostawiania do powyższych liczb, liczb przestępnych. Celem pokrycia niezgodności w obliczeniach roku kalendarzowego. Przy okazji tych obliczeń, stworzyłem na swoje potrzeby taki układ z liczb pierwszych. (poniżej)
I tutaj się zdziwiłem, bo nauka twierdzi, że liczby pierwsze w układzie ze złożonymi, tworzą zupełnie przypadkowy szereg, jakby bez jakiegokolwiek sensu. Naukowcy dociekają, gdzie on jest? Bo przecież nic w naturze nie jest bez logiki i wszystko jest matematyką.
Niech mi teraz ktoś powie, że nie widać tutaj naocznie pewnej systematyki! Jakby układu 2-kowego
Warto rozważyć, czy nie kłania się tutaj, występujący w naturze złoty podział.
Liczby pierwsze, to takie, które się dzielą TYLKO przez dwie liczby; 1-en oraz przez siebie samą.
Nie jest więc nimi 1-ka, bo ma tylko jeden, ten sam dzielnik.
Liczby: 4, 6, 8, 9, nie są liczbami pierwszymi, a złożonymi.
Do liczb pierwszych, należą, oznaczone przeze mnie bez nawiasu.
Uporządkowałem je w kolumnie, według rzędu wyznaczonego przez jedną liczbę pierwszą.
Dla uproszczenia, wszystkie liczby poza pierwszymi, nazywam niepierwszymi.

Cechy takiego logicznego porządku liczb pierwszych i niepierwszych.
1) Każdy rząd licz niepierwszych, zaczyna się jedną liczbą pierwszą.
2) Wszystkie przeskoki w rzędzie, liczb niepierwszych , następują o dwie liczby niepierwsze, do przodu lub do tyłu, lub o cztery liczby niepierwsze. Zawsze więc o parzystą ilość liczb niepierwszych. Wyznacza je bok trójkąta.
3) W liczbach rozpatrzonych, każdy bok trójkąta obejmuje równo 2 liczby, do punktu załamania.
4) Rzędy liczb, rozdzielają rzędy liczb niepierwszych w ilości nieparzystej; 1, 3 itd… Lewy stożek trójkąta zawsze wskazuje liczbę nieparzystą!
5) W miejscu do trzynastki włącznie, mamy 10 poziomów/rzędów liczb niepierwszych.
6) Końce trójkąta po prawej stronie liczą dla liczb w rzędzie oznaczonych pionową linią przerywaną, której maksimum od lewego wierzchołka trójkąta liczy 5 liczb, liczą do liczby 89 w kolejnym rzędzie, 7-em rzędów.
7) Końce trójkąta po prawej stronie, dla liczb oznaczonych pionową linią kropkowaną, której maksimum liczb od lewego wierzchołka trójkąta posiadają 3-y liczby niepierwsze, liczą również 7-em rzędów.
8) Końce boku trójkąta po lewej stronie, dotykające pojedynczej liczby niepierwszej, liczą 7-em rzędów.
9) Wszystkie lewe wierzchołki trójkątów, w przypadku dwóch liczb na wierzchołku (pierwszych łącznie z niepierwszymi), liczą 7-em rzędów!
10) Po lewej stronie tych linii, mamy pionowo, tylko rząd cyfr parzystych.
11) Zaś po ich prawej stronie – przyległej, tylko pionowy rząd cyfr nieparzystych.
- Liczby po skrajnej stronie prawej (końcowe ), zawsze są o jedną mniejsze niż liczby końcowe po stronie lewej. Np.; 10 – 11, 16 – 17, 22 – 23, 28 -29, itd. …
- Kiedy dodamy do siebie liczby z rzędu oznaczonego liczbą 7 (bez liczby 7), uzyskując sumę 27, po jej podziale według zasady „złotego podziału”, otrzymamy dwie składowe złotego podziału (bez ułamków, z racji nie występowania w układzie ułamków), w postaci 10 i 16. Znajdziemy je na prawym wierzchołku rzędu z którego pobraliśmy zsumowaną liczbę oraz na wierzchołku prawego trójkąta poniżej.
- Kiedy z rzędu 23 zszumujemy liczby; 28, 27, 24, dzieląc ich sumę zasada złotego podziału, uzyskamy w przybliżeniu liczby 24 i 30. Znajdują się one w tym samym rzędzie pionowym
- Kiedy z rzędu 23 zsumujemy inny ciąg ograniczony uskokami; 26, 25, 24, to z podziału ich sumy 75, uzyskamy liczby złotego podziału, w prawym wierzchołku uskoku 46 i wierzchołku 28.
Wniosek? Wydaje się, że układ faluje odcinkami złotego podziału.
(tu można wyliczać te proporcje;https://calcoolator.pl/zloty_podial_zlota_proporcja.html )
https://encrypted-tbn0.gstatic.com/images?
Zauważmy, że w złotym podziale, 2-ka występuje rzadko, za to 1-ka licznie.
Ma on odniesienie, nawet do budowy człowieka i ciągu Fibonacciego.
q=tbn:ANd9GcQGpAqYYOdkKHriHrJq0Fue8EQz6yNM9qRbSuKZxJZ7MkSTtb7DGQ
https://pl.wikipedia.org/wiki/Z%C5%82oty_podzia%C5%82
Może więc układ liczb pierwszych, prawidłowo ustawiony, oddaje zasadę złotego podziału?
Za dużo jest tutaj porządku, systematyki, aby było to przypadkowe!
- Wszystkie liczby pierwsze, poza 2-ką, są liczbami nieparzystymi. Co jest nie tak, z tą 2-ką? Jakoś mi nie pasuje do tego układu. Może po jej odjęciu i włączeniu 1-ki, zloty podział byłby jeszcze precyzyjniejszy i układ bardziej regularny?
- Kiedy do załączonej na rysunku figury Pentagonu, wstawimy punkty o regularnych, równych odstępach X , jak proponowane przeze mnie liczby pierwsze; A=1, B=3, C=5, D=7, to uzyskamy podobną figurę według zasady złotego podziału. Wypadający poza linią punkt narożny nie oznaczony, odpowiada liczbie 9 nie należącej do liczb pierwszych.
Dlatego, aby układ był całkowicie zgodny, sensowny, należałoby zmienić jego początek. Tak jak na moim rysunku niżej.
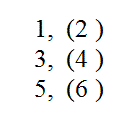
Taki układ, zaczynałby się 1-ką jako liczbą pierwszą. Nie może? Kwestia logiki… Przecież liczba 1 dzieli się przez dwie; 1 i 1. Te same liczby, lecz w dwóch znaczeniach; przez siebie i przez pierwszą liczbę układu. Może tu jest sens?
Pasuje mi wrzucenie 2-ki w pionowy szereg liczb niepierwszych. Bo wówczas, znajdzie się ona w pierwszym rzędzie pionowym liczb parzystych. Zachowując logikę dalszej części układu. Tyle tylko, że liczba 2 dzieli się przez siebie i 1. I przez nic więcej! Miałby to być jakiś wyjątek?
Ale zauważmy, że nastąpiłaby tutaj zamiana; liczba 1 jako pierwsza, zaś 2 jako niepierwsza.
Dlaczego 2 pasuje mi wyraźnie tutaj do pionu liczb niepierwszych?
Wydaje mi się, że aby rozwiązać problem rzekomego nieuporządkowania liczb pierwszych (przypadkowości), należałoby zmienić ich regułę. Tak, aby rozrysowany przeze mnie początek układu oraz jego reszta, były ze sobą zgodne. Nieco ją rozszerzyć,o jedną zasadę.
Reguła liczb pierwszych, brzmiała by wówczas:
„Liczbą pierwszą jest liczba, która dzieli się tylko przez siebie oraz przez 1-en i jest liczbą nieparzystą”.
Liczba 1-en spełniałaby wówczas wszystkie trzy warunki.
Liczba 2, nie spełniałaby jednego warunku – bo jest parzysta.
Układ, byłby wówczas uporządkowany całkowicie i logiczny od początku!
Wszystkie liczby, podobno powstają z liczb pierwszych, aktualnie za takie uznawanych.
Np. 5 x 51 = 255, (Uwaga; nieważne, że 51 zawiera liczbę niepierwszą 1)
To jednak nieprawda, bo są wyjątki, łamiące tą regułę!
Bo 3 nie powstanie z mnożenia czy dodania innych liczb pierwszych.
Tylko zawsze, z zastosowania liczby 1 !
3 ; 1 + 1 + 1 = 3 lub 1 x 3 = 3
Podobnie liczba pierwsza 2.
Bo powstaje tylko w wyniku 1 + 1 =2, lub 1 x 2 = 2
Skoro 1 nie jest liczbą pierwszą a 2 i 3 jest, to nie powinniśmy wykonać równania (1) + 2 = 3
Są tutaj więc poważne, sztuczne ograniczenia. Doktryna, zapewne mylna, nie konsekwentna.
Taka z przyzwyczajenia naukowców do czegoś, co zaszło już daleko…
Natomiast każdą liczbę stworzymy z operacji na liczbach naturalnych. To jest prawda. Ale nie pierwszych, jeśli nie zaliczymy do niej 1-ki!
A co się stanie, jeśli tak, jak proponuję, wypadnie nam 2-ka do tej pory będąca liczbą pierwszą?
A zastąpimy ją 1-ką? Wówczas, stworzymy wszystkie liczby do 10-ciu i dalej, z wykorzystaniem tylko liczb pierwszych; 1, 3, 5, 7 ! Bo 1-ka zawsze będzie nas ratować Gdzie 1-kę uznaliśmy za liczbę pierwszą zamiast 2-ki, wykluczonej z układu?
Moim zdaniem, nie można definiować liczb pierwszych ich tworzeniem innymi liczbami, przez mnożenie, bo zawsze będą wyjątki.
Liczby pierwsze tworzone są przez liczby naturalne. 1-ka spełnia ten warunek, bo też jest taką liczbą. Niekiedy, nawet 0 uznaje się za liczbę naturalną.
Wydaje się zbyt proste? A może takie powinno być?
Tylko uznanie 1-ki za liczbę pierwszą, umożliwi nam pełne spełnienie warunku budowy wszelkich liczb za pomocą liczb naturalnych lub pierwszych, z wynikiem w postaci pełnych liczb, poprzez mnożenie.
Zaś wykluczenie 2-ki (dla uzyskania regularności układu), z ciągu liczb pierwszych, nie powoduje jego załamania i nie uniemożliwia tworzenia tej liczby przez mnożenie.
Wiemy, że liczby pierwszej nie da się rozbić na iloczyn mniejszych liczb naturalnych. Na przykład 6 = 2 × 3, da się je rozbić. Zauważmy, że to iloczyn dwóch liczb pierwszych. Rozbiliśmy 6 na czynniki pierwsze. Liczby 7 nie da się tak rozbić. Można tylko napisać, że 7 = 1 × 7 A to przecież nie jest rozbijanie, bo 7 jest jak było. Tymczasem 6 dało się rozbić. 4 też da się rozbić jako 2 × 2.

Zauważmy, że w nowym układzie, aż do pozycji liczby 9 (niepierwszej), liczby zmieniają się regularnie, co jedną. To wprowadzenie systematyki układu już na jego początku. I wynika tylko z dopisania do definicji, że nie mogą to być liczby parzyste! I włączenia 1-ki do układu, zgodnie z definicją. Bo warunek dzielenie się liczby pierwszej przez siebie oraz jeden, nie mówi, że dzielnikiem ma być zawsze inna liczba!
Może należy więc skończyć z twierdzeniem, że liczba pierwsza to liczba naturalna większa od 1? Niepotrzebny dodatek, wykluczający ta liczbę tylko z początku układu. Pozostały warunek, że ma ona tylko dwa dzielniki naturalne – jedynkę i samą siebie, oraz jest nieparzysta, byłby prawidłowy.
Żadnej liczby pierwszej z pierwszego szeregu; 2,3,5,7, nie przedstawi się w prostym działaniu, za pomocą iloczynu (mnożenia) liczb pierwszych (bez jedynki), bo z założenia liczba pierwsza ma tylko 2 dzielniki: liczbę pierwszą (samą siebie) i 1 (liczbę niepierwszą). I są nieparzyste (poza dwójką), co przy nieużywaniu w mnożeniu 1, dałoby wynik nieprawidłowy. Jeśli natomiast dodamy 1 do pierwszych, to się je poprzez mnożenie przedstawi.
Problemem liczb pierwszych i wynikającej z tego częściowej niedokładności (przypadkowości) układu liczb pierwszych, są więc dwie liczby z początku układu. Uznana za pierwszą 2 która nią nie jest oraz 1 której za pierwszą nie uznano. Odwrócenie ich roli, może ten problem rozwiązać.
Co ciekawe, powstanie wtedy system 1-ko – 2-kowy, czyli pełny. Jak w informatyce, gdzie mamy 0 – 1-kowy. Przestrzenny. Bo chociaż 2-ka będzie po stronie liczb niepierwszych, to układ będzie dawał dalej wyniki o dwa stopnie przesunięte.
- No i jeszcze wróćmy do naszej słowiańskiej 12-ki. Otóż zaproponowany przeze mnie układ,
rozpoczynałby się tak; 1 (2), czyli liczba pierwsza 1 i liczba niepierwsza 2. Jakby dwa po przecinku; 1,2 lub po przesunięciu zera, jako 12-cie. Może i to ma jakiś ważny, ukryty sens?
https://www.tajemnice-swiata.pl/ciag-fibonacciego/
Rafał Kopko – Orlicki
Warszawa, 2018.12.09
Źródła:
Cytat: „Teraz wydaje się jednak, że jakaś reguła, choć być może z elementem losowości, w rozkładzie liczb pierwszych obowiązuje. Na razie nikt nie ma pojęcia, na czym polega ta prawidłowość i czy może dzięki niej uda się zgłębić więcej tajemnic tych elementarnych liczb. Do tej pory nikt nie dowiódł na przykład hipotezy Goldbacha – że każda liczba parzysta większa od 2 może być przedstawiona w postaci sumy dwóch liczb pierwszych. „
http://www.deltami.edu.pl/temat/matematyka/teoria_liczb/2012/03/27/Zlozony_problem_liczb_pierwszych/
https://pl.wikipedia.org/wiki/Liczba_pierwsza
https://pl.wikipedia.org/wiki/Z%C5%82oty_podzia%C5%82
https://www.nlogo.pl/wiedza/czym-jest-zloty-podzial
Kolejny Cytat:
„Witam. Rozkład w przestrzeni 2D za pomocą Spirali Ulama oraz Krzyża Plichty zainspirował mnie do trochę innej wariacji z liczbami pierwszymi w przestrzeni.
Liczby pierwsze w prostej geometrii.
Chciałbym zaprezentować, że tak powiem – metodę filtrowania liczb pierwszych.
Nazwałem ją „filtrowaniem pentagonalnym”.
Pomysł jest bardzo prosty.
Należy rozstawić na wierzchołkach pięciokąta kolejne liczby
naturalne. (czyli 1,2,3,4,5,6,7 itd.)
Liczby pierwsze będą rozchodziły się z dość ciekawą regularnością.
Każda liczba pierwsza na danym kierunku (z danego kąta tego pięciokąta).
będzie większa od poprzedniej o dziesietną wartość wynoszącą 5, 10, 20, 30 i tak dalej.
Każda kolejna liczba pierwsza zachowa wartość jedności taką samą jak poprzednia liczba.
Na przykład: 2, 7, 17, 37, 47, 67, 97, 107 i tak dalej. (wyjątkiem jest pierwsza liczba pierwsza czyli 2).
To jest oczywista regularność. To jest pewien wzór w zbiorze liczb pierwszych.
Moim zdaniem ta regularność wynika z właściwości pięciokąta, w którym kąt jego ramion to 72 stopnie.
W pięciokącie, jego obwód do przekątnej (ale nie tej przechodzącej przez geometryczny środek) ma stosunek wynoszący Phi. (1.618).
Phi jest złotą liczbą stosowaną w złotym podziale.
To wskazuje moim zdaniem na związek zbioru liczb pierwszych ze złotym podziałem.
Wskazuje też, że nie ma przypadkowości w tym zbiorze liczb pierwszych. Eksperyment dokonałem na pierwszych 500 liczbach naturalnych i sądzę, że ta prawidłowość występuje do nieskończoności.
Może kogoś to zainspiruje do dalszych prac na tymi liczbami i/lub okaże się w ogóle pomocne. Pozdrawiam.”
Tekst zamieściłem też na moich stronach.
Linki do pomocnych filmów
Film pierwszy pokazuje o sztuczności, a więc być może nieprawidłowość wykluczenia liczby 1 z grupy liczb pierwszych. Drugi błąd,to przypisanie 2 do liczb pierwszych.
Złamanie kodu systematyczności liczb pierwszych, zlikwiduje (jak mówi film), możliwość szyfrowania. Otworzy również drogę do pełnego wykorzystania fizyki kwantowej.
RKO
http://home.agh.edu.pl/~zobmat/2017/wyr_swierkotmarek/hipoteza.html
